Graph-based SLAM using Pose-Graph

 

[SLAM] Graph-based SLAM (Pose graph SLAM) · Jinyong

 

Cyrill Stachniss 교수님 Lecture

지금까지 다양한 Kalman Filter Series를 다뤄보았는데 사실 SLAM을 다룰때는 거의 사용되지 않는다고 합니다. 현재 SLAM은 대부분 Graph-based SLAM 이라고 하는데 어떤 컨셉으로 수행되고 어떤 차이가 있는지 알아보도록 하겠습니다.

Graph Based SLAM

Graph-Based SLAM

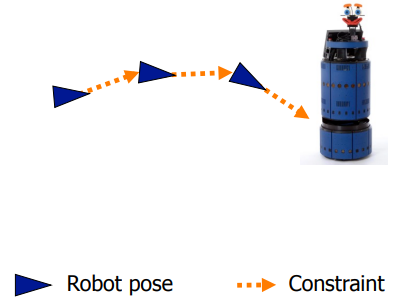
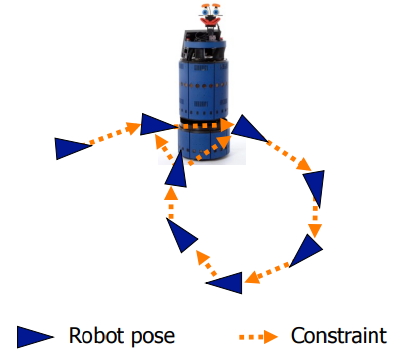
로봇은 움직이면서 자신의 pose(x, y, z, orientation 등)가 변화하게 됩니다. 이렇게 움직이면서 자신의 pose를 IMU나 GPS와 같은 센서로 Tracking 할 수 있습니다. 그와 동시에 주변환경을 카메라나 LiDAR로 인식 할 수 있습니다. Graph-Based SLAM 에서 Pose Graph는 로봇이 움직이면서 Tracking 한 pose(Node)와 pose들 사이의 Constraint(Edge)를 저장합니다. Graph-Based SLAM은 직역 그대로 문제를 graph로 표현해 해결합니다.

Graph-Based SLAM example

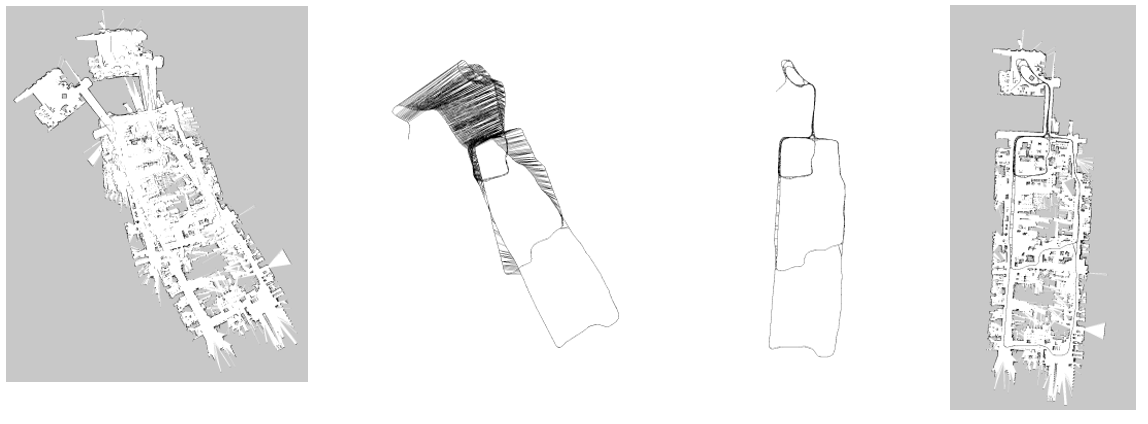
위 그림의 맨 좌측은 로봇이 측정한 자신의 위치에서 주변환경을 레이저로 측정한 map입니다. 하지만 로봇은 자신의 Global 위치, orientation 등을 추정할 순 있지만 정확히 알 수 없기 때문에 오차가 발생합니다. 만약 자신의 pose를 보정해 오차를 줄인다면 오른쪽처럼 보다 정확한 map을 얻을 수 있습니다. 

 

Pose Graph

Constraint between adjacent nodes

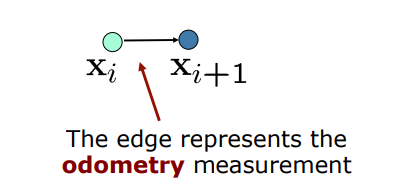
위 그림처럼 로봇이 \(x_{i}\) 에서 \(x_{i+1}\)로 움직인다면 odometry 정보를 얻어서 노드간의 Constraint를 얻어낼 수 있습니다. 

Constraint between non-adjacent nodes

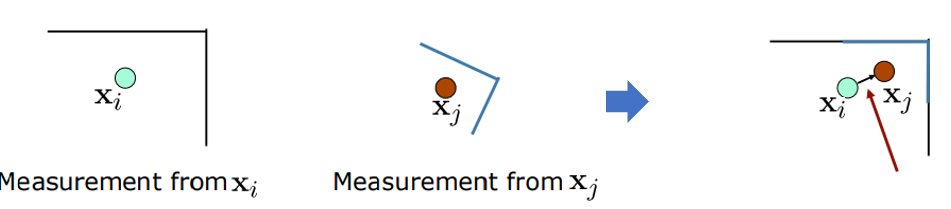
위 그림은 노드간의 Constraint를 얻을 수 있는 또 다른 방법을 보여줍니다. 1) \(x_{i}\), \(x_{j}\) 두 지점에서 같은 Corner를 관측하고, 2) 같은 Corner라는 것을 알 수 있다면, ICP(Iterative Closest Point)와 같은 방식으로 observation을 overlap 해줍니다. 이렇게 되면 \(x_{i}\) 의 관점에서 \(x_{j}\)의 pose를 추정할 수 있습니다. 

Difference of Virtual measurement and Pose Graph

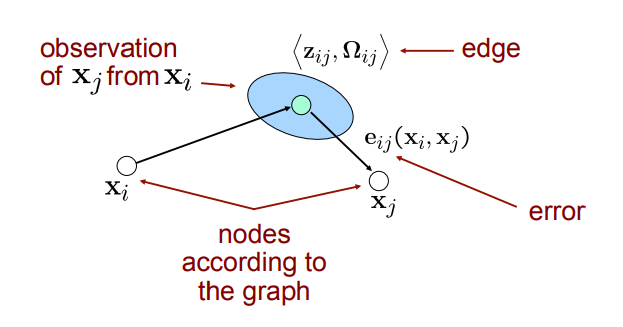
이렇게 되면 위 그림처럼 \(x_{j}\)에 대한 정보는 1) \(x_{i}\) 의 관점에서 본 \(x_{j}\)의 pose 와 2) Graph node 에 따른 \(x_{j}\) 의 pose를 갖게됩니다. 따라서 오차 \(e_{ij}(x_{i},x_{j})\)를 줄이는 방향으로 pose를 보정해나갑니다.

 

Least Squares

Least squares approximation 이란 어떤 계의 해방정식을 근사적으로 구하는 방법으로, 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법입니다(Wiki).

 

오차를 최소화하기 위해선 우선 error function 을 알아야합니다. 

$$e_{ij}(x_{i},x_{j}) = t2v(Z^{-1}_{ij}(X^{-1}_{i}X_{j}))  $$

 

\((X^{-1}_{i}X_{j})\) 는 \(x_{i}\)를 좌표계의 원점으로 두고 본 \(x_{j}\)를 의미합니다. \(Z_{ij}\)는 ICP로 정보를 overlap 해서 만든 \(x_{j}\) 입니다. 따라서 이 수식을 해석해보면 graph의 정보를 토대로 \(x_{j}\)로 transform 후 ICP 정보를 통해 다시 \(x_{i}\)의 위치(inverse of Z)로 돌아오는 것입니다. 만약 두 transformation이 일치하지 않는다면 처음 출발한 자리로 돌아가지 못하고 어느정도의 오차가 낀 곳에 위치할 것입니다.

 

$$ e_{ij}(x+\Delta x) \simeq  e_{ij}(x) + J_{ij}\Delta x $$

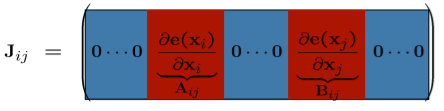
오차가 최소화되는 방향으로 최적화를 진행하기 위해 error function을 Taylor expansion을 이용해 선형화합니다. \(e_{ij}\) 는 모든 pose가 아닌 \(x_{i}\), \(x_{j}\)에만 영향을 받기때문에 Jacobian 행렬은 이 두 index를 제외한 나머지 부분은 0인 희소행렬이 됩니다.

Jacobian matrix

 Optimization

Optimization Algorithm

Jacobian 행렬 \(J_{ij}\)는 최적화에 필요한 \(b\) 와 \(H\)를 구하는데 사용됩니다. 

Coefficient b and Information matrix H

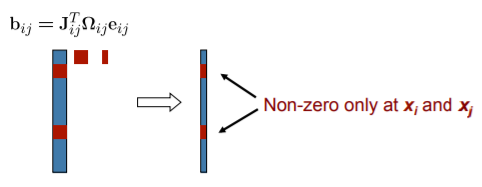
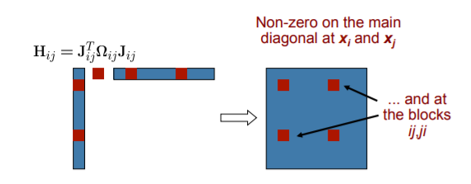
Jacobian 행렬이 희소하기 때문에 single constraint에 대한 \(b_{ij}\), \(H_{ij}\) 모두 희소행렬이 됩니다. 모든 constraint에 대한 \(b\) 와 \(H\)를 구하면 각각 dense 벡터와 희소행렬의 형태가 될 것입니다. 이 희소성이 실제 연산을 수행할 때 효율적으로 연산을 수행할 수 있게 합니다.