여러 종류의 칼만필터(Family members of Kalman Filter)(EKF)
Jinyong 님 블로그 [SLAM] Kalman filter and EKF(Extended Kalman Filter) · Jinyong [SLAM] Kalman filter and EKF(Extended Kalman Filter) Kalman filter와 Extended Kalman filter에 대한 설명. 본 글은 Uni..
jml-note.tistory.com
Cyrill Stachniss EKF SLAM Lecture
GitHub - AtsushiSakai/PythonRobotics: Python sample codes for robotics algorithms.
Python sample codes for robotics algorithms. Contribute to AtsushiSakai/PythonRobotics development by creating an account on GitHub.
github.com
이전에 State estimation 을 위한 Extended Kalman Filter 포스팅을 올렸었습니다. 여기서 말하는 State estimation은 로봇이 움직이고 자신이 움직인 위치를 추정하는 Localization을 말합니다. SLAM이란 Simulatneous Localization and Mapping으로 로봇이 자신의 위치를 tracking하는 동시에 주변 환경의 지도를 구축, 업데이트 하는 문제를 말합니다.
EKF SLAM
EKF SLAM은 Extend Kalman Filter를 적용한 SLAM을 말합니다. SLAM 문제를 해결하기 위한 최초의 모델로 80년대 쯤 나온 방법이고 요즘은 거의 쓰지 않는다고 하지만 SLAM을 접근하는 컨셉을 알아보기 위해 스터디를 해보겠습니다.
Given
- The sent controls commands, \( u_{1:T} = \{u_{1},u_{2},...,u_{T}\}\)
- Observations, \( z_{1:T} = \{z_{1},z_{2},...,z_{T}\}\)
Wanted
- Map of the environment \( m\)
- Path(or current pose) of the vehicle, \( x_{0:T} = \{x_{0}, x_{1},...,x_{T}\}\)

문제 정의를 해보면 우리는 로봇의 컨트롤과 센서로 얻은 정보로 부터 로봇의 주변환경과 이동경로를 얻어내야 합니다. 전체 이동경로를 구하고 싶다면 offline SLAM, 현재 위치만 구하고 싶으면 online SLAM이라고 합니다. 저는 online SLAM을 가정하도록 하겠습니다. Offline SLAM 은 loop closure가 수행되면 전체 경로가 보정되어야하지만 online SLAM의 경우는 이전 trajectory는 고려하지 않습니다. 그리고 2D plane에서의 SLAM을 가정하면 State 벡터는 Robot의 state과 Landmarks 들을 포함합니다.
$$ x_{t} = \{x,y,\theta, m_{1,x},m_{1,y}, ... , m_{n,x},m_{n,y}\}^{T}$$
여기서 또 하나 필요한 가정은 랜드마크를 관측하면 그 랜드마크가 어떤 랜드마크인지 알고있다는 것입니다.
State Representation
이전 포스팅에서 다룬 Extended Kalman Filter의 step을 그대로 밟아가면서 SLAM이 어떤식으로 수행되는지 알아볼 것입니다. 다만 EKF는 Localization만을 봤다면 SLAM은 mapping을 같이 보기 때문에 우리가 구하고자 하는 \(\mu\), \(\Sigma\) 가 어떻게 확장되었는지 보겠습니다.

\(\mu \)은 로봇의 pose와 랜드마크의 위치정보를 의미합니다. 2D 환경에서의 SLAM을 가정하고 있기 때문에 \(\mu \)는 \(x,y,\theta \) 와 n개의 랜드마크의 \(x,y\)좌표를 갖고 따라서 \( 3+2n \) 의 벡터가 됩니다. 따라서 Uncertainty를 의미하는 Covariance matrix \(\Sigma \)는 \((3+2n)^{2}\) 크기의 행렬이 됩니다.
EKF-SLAM

EKF SLAM Setup
- Robot moves in the 2D plane
- Velocity-based Motion Model
- Observation of point landmarks
- Range-bearing Sensor
- Known data association
- Knonw number of landmarks
문제를 단순화하기 위해 위의 리스트들을 가정합니다.
Initialization

최초의 로봇의 위치를 원점으로 가정한다면 랜드마크들에 대한 관측값이 없기 때문에 state vector는 0벡터로 초기화 해줍니다. Covariance 행렬의 경우 landmark에 대한 uncertainty는 infinity로 초기화하고 나머지 값들은 전부 0으로 초기화해줍니다. EKF의 과정을 그대로 따라가며 mean과 covariance를 업데이트를 하면 EKF-SLAM 이 됩니다.
로봇이 움직이게 되면 Pose에 대한 covariance, 즉 uncertainty가 증가하게 됩니다. 따라서 위 그림과 같이 pose와 관련된 covariance들이 증가할 것입니다.
Prediction Step
Mean Prediction

로봇의 motion model이 위의 수식을 따른다고 가정하면 위 과정 자체가 mean prediction이 됩니다.
Covariance Prediction
EKF의 내용을 잠깐 복기해보면 linear model 에서만 적용가능한 Kalman Filter의 한계를 극복하기 위해 Tayler expansion을 이용해 함수를 선형화해줬습니다. 따라서 EKF Algorithm의 \(G_{t} \)는 motion model의 Jacobian Matrix가 되게 되는데 우리가 사용하는 Covariance Matrix는 \((3+2n)^{2}\)의 행렬이기 때문에 \(G_{t} \)를 다음과 같이 정의합니다.
위에서 언급했듯이 covariance matrix는 \((3+2n)^{2}\)의 행렬인데 로봇 state 변화는 landmark에 아무 영향을 주지 않기 때문에 다음과 같이 정의됩니다.
$$ G_{t} = \begin{bmatrix} G_{t}^{T} & 0 \\ 0&I \end{bmatrix} $$
따라서 motion model \(g \) 의 Jacobian 을 구하면 Prediction step 완료됩니다.
Correction Step
Correction Step에서 하는 일은 실제 관측과 예측되는 관측값의 차이를 이용해 predicted state를 보정하는 것입니다. 위에 Setup에서 센서는 Range-bearing 센서를 이용한다고 가정했습니다. 실제 관측값을 \(z_{t}^{i} = (r_{t}^{i},\phi_{t}^{i} )\) 로 정의합시다.
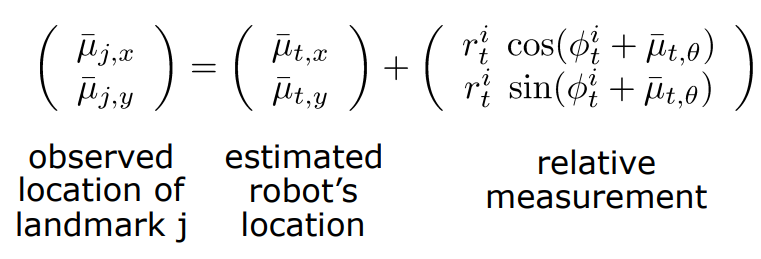

예측 관측값은 위 수식처럼 쉽게 구해낼 수 있습니다. Observation model \( \hat{z}_{t} = h(\bar{\mu}_{t,\theta})\) 의 Jacobian Matrix를 계산하면 Kalman Gain 을 구하기 위한 \(H_{t}\)를 구할 수 있습니다.
'SLAM' 카테고리의 다른 글
| Graph-based SLAM using Pose-Graph (0) | 2021.10.10 |
|---|---|
| EKF SLAM with Example Code (0) | 2021.09.23 |
| 여러 종류의 칼만필터(Family members of Kalman Filter)(EnKF) (0) | 2021.08.19 |
| 여러 종류의 칼만필터(Family members of Kalman Filter)(UKF) (0) | 2021.08.10 |
| 여러 종류의 칼만필터(Family members of Kalman Filter)(EKF) (0) | 2021.08.03 |



댓글