[SLAM] Kalman filter and EKF(Extended Kalman Filter) · Jinyong
[SLAM] Kalman filter and EKF(Extended Kalman Filter) Kalman filter와 Extended Kalman filter에 대한 설명. 본 글은 University Freiburg의 Robot Mapping 강의를 바탕으로 이해하기 쉽도록 정리하려는 목적으로 작성되었습니다.
jinyongjeong.github.io
Kalman Filter & EKF (Cyrill Stachniss)
이전 포스팅에서는 비선형모델에서 가우시안 모델을 이용해 상태 추정하기 위한 EKF(Extended Kalman Filter)를 알아보았습니다. EKF에선 비선형 모델을 선형화하기 위해 Taylor Expansion을 이용했습니다. EKF에서 선형화의 과정은 가우시안 분포가 입력으로 들어왔을 때 출력 역시 가우시안 분포를 얻기 위해서입니다. 가우시안 분포를 유지하는 다른 방법은 없을까요?
UKF(Unscented Kalman Filter)

EKF는 비선형함수를 Talyer expansion을 통해 선형화해 가우시안 분포를 유지합니다. 하지만 이 경우 mean 주변에서 선형화가 되어 정확한 estimation이 어려울 수 이습니다.

UKF 에서는 함수를 선형화하지 않고 여러 샘플을 통해 가우시안의 근사분포를 얻어내는 것을 목표로 합니다. 이 샘플들을 비선형 함수를 통해 Transform을 수행하면 기존의 가우시안 분포가 유지되지 않기 때문에 분포형태가 깨지게됩니다. 결과 point들의 새로운 mean값과 covariance를 계산해 새로운 가우시안 분포를 만드는 것이 UKF의 목적입니다.
4-step Unscented Kalman Filter
- Compute sigma points
- Compute sigma points' weight
- Perform transform through non-linear function
- Compute gaussian from weighted points
UKF를 수행하기 위해선 첫째로 샘플로 사용할 점을 정해야합니다. 이때 샘플로 정하는 point들을 Sigma point χ[i], weight w[i]를 구하는데 global rule은 다음과 같습니다.
∑iw[i]=1
μ=∑iw[i]χ[i]
Σ=∑iw[i](χ[i]−μ)(χ[i]−μ)T
하지만 위 제약사항을 만족하는 χ[i], weight w[i]는 유일하지 않기 때문에 위의 제약사항을 만족시키면서 좋은 Sigma point를 정하는 것이 중요합니다.
Choosing Sigma Points
χ[0]=μ
χ[i]=μ+(√(n+λ)Σ)i for i=1,…,n
χ[i]=μ−(√(n+λ)Σ)i−n for i=n+1,…,2n
선정하는 Sigma point의 개수는 가우시안의 dimension n에 의해 결정됩니다. 위 수식에서 n 이 1이면 sigma point는 μ 1개와 1×2로 3개, 2차원이면 5개를 선정합니다. μ를 중심으로 샘플을 뽑는다고 생각하면 직관적으로 받아들이기 쉽습니다.
λ는 μ에서부터 샘플을 얼마나 먼 지점에서 뽑느냐를 결정하고, 수식의 인덱스 i (아래첨자)는 행렬의 열벡터를 의미합니다.
수식에서 n, λ는 스칼라 값이므로 √Σ를 계산해야합니다. 행렬의 제곱근은 다음과 같이 정의합니다
Σ=SS
S=√Σ
1. Decomposition via diagonalization

행렬의 제곱근을 구하는 방식 중 하나는 대각화를 이용하는 것입니다. 위 수식처럼 분해를 하게 되면 S=VD1/2V−1로 정의할 수 있습니다.
2. Cholesky decomposition
Σ=LLT
L=√Σ
Cholesky Decompostion은 수치적으로 더 안정적이기 때문에 UKF 구현에 자주 사용된다고 합니다. 이 경우 행렬의 제곱근을 위 수식처럼 정의하고 수식을 전개해나갑니다. Cholesky decomposition - Wikipedia.
Computing sigma point weights
w[0]m=λn+λ
w[0]c=w[0]m+(1−α2+β)
w[i]m=w[i]c=12(n+λ)
Sigma point 에 대한 가중치는 위 수식과 같이 계산됩니다. 가중치는 mean을 계산하기 위한 wm과 Σ를 계산하기 위한 wc 두 종류가 필요합니다. 그 중 μ에 대한 각각의 가중치를 구하는 것이 첫 두 수식이고 나머지 sigma point에 대한 가중치는 세번째 수식처럼 구해집니다.
Gaussian Approximation
가우시안 분포는 mean μ 와 covariance Σ 로 표현되기 때문에 위에서 구한 Sigma point 와 그에 해당하는 가중치를 구한 순간 가우시안 분포를 얻었다고 볼 수 있습니다.
μ′=2n∑i=0w[i]mg(χ[i])
Σ′=2n∑i=0w[i]c(g(χ[i])−μ′)(g(χ[i])−μ′)T
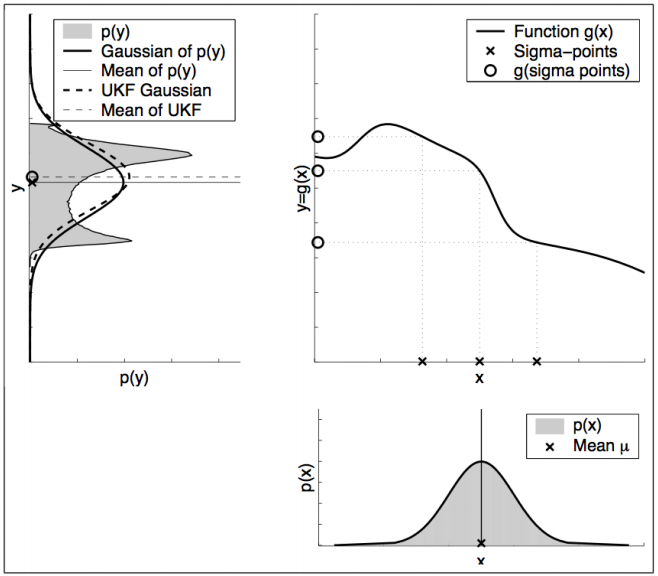
결과적으로 실제 위 그림에서 p(y)의 가우시안에 근사한 UKF 가우시안 분포를 만들어 낼 수 있습니다. 이렇게 구한 가우시안 분포가 EKF에서 Tayer Expansion을 통해 선형화한 함수로 Transform한 가우시안 분포보다 정확합니다.
UKF Algorithm
def main():
print(__file__ + " start!!")
nx = 4 # State Vector [x y yaw v]'
xEst = np.zeros((nx, 1))
xTrue = np.zeros((nx, 1))
PEst = np.eye(nx)
xDR = np.zeros((nx, 1)) # Dead reckoning
wm, wc, gamma = setup_ukf(nx)
# history
hxEst = xEst
hxTrue = xTrue
hxDR = xTrue
hz = np.zeros((2, 1))
time = 0.0
while SIM_TIME >= time:
time += DT
u = calc_input()
xTrue, z, xDR, ud = observation(xTrue, xDR, u)
xEst, PEst = ukf_estimation(xEst, PEst, z, ud, wm, wc, gamma)
# store data history
hxEst = np.hstack((hxEst, xEst))
hxDR = np.hstack((hxDR, xDR))
hxTrue = np.hstack((hxTrue, xTrue))
hz = np.hstack((hz, z))PythonRobotics 의 예제를 가져와봤습니다. main 부터 간단히 살펴보면 Kalman Filter에서 필요한 변수들을 초기화합니다. 예제에서 state vector는 [x,y, yaw, v]로 nx(state의 차원) 4입니다. xEst ,xTrue, xDR는 각각 UKF, ground truth, dead reckoning 으로 얻을 state을 저장하는 변수입니다. PEst는 Covariance를 저장하는 변수인듯 합니다.
최초의 state을 0, Covariance Matrix를 Identity matrix로 두고 setup_ukf에서 ukf 파라미터를 설정해줍니다.
def setup_ukf(nx):
lamb = ALPHA ** 2 * (nx + KAPPA) - nx
# calculate weights
wm = [lamb / (lamb + nx)]
wc = [(lamb / (lamb + nx)) + (1 - ALPHA ** 2 + BETA)]
for i in range(2 * nx):
wm.append(1.0 / (2 * (nx + lamb)))
wc.append(1.0 / (2 * (nx + lamb)))
gamma = math.sqrt(nx + lamb)
wm = np.array([wm])
wc = np.array([wc])
return wm, wc, gammalamb(λ) 는 가우시안 mean과 sigma point간의 거리를 결정하는 변수입니다. 그리고 lamda는 α, κ에 의해 결정됩니다.
그리고 UKF에서 필요한 두 종류(mean, covariance)의 weights 을 초기화합니다. 입력 가우시안 분포의 mean에 해당하는 weight과 나머지 sigma point에 해당하는 weight을 다르게 초기화하는 것을 알 수 있습니다. 변수 gamma는 √n+λ 스칼라 값을 저장합니다.
다시 main으로 돌아가면 while문에서 time을 증가시키며 ukf를 통해 state를 업데이트합니다. 변수 u는 predefined된 control input입니다.
def calc_input():
v = 1.0 # [m/s]
yawRate = 0.1 # [rad/s]
u = np.array([[v, yawRate]]).T
return ucalc_input을 보면 속력 v 는 1로 일정하고 z축 회전 yaw는 0.1로 설정되어있네요. 만약 노이즈가 없는 완벽한 이동을 한다면 로봇은 원을 그리는 운동을 할 것이라는 것을 추측할 수 있습니다.
def observation(xTrue, xd, u):
xTrue = motion_model(xTrue, u)
# add noise to gps x-y
z = observation_model(xTrue) + GPS_NOISE @ np.random.randn(2, 1)
# add noise to input
ud = u + INPUT_NOISE @ np.random.randn(2, 1)
xd = motion_model(xd, ud)
return xTrue, z, xd, udobservation에서는 관측값 z를 얻는것이 목적입니다. Ground Truth를 의미하는 변수 xTrue에 노이즈가 없는 control u를 이용해 업데이트를 해주는 것을 볼 수 있습니다. 그리고 z는 실제위치에서의 관측값을 저장합니다.
하지만 실제로는 control 자체가 완벽하지 않기 때문에 이 시점에서 로봇이 생각하는 자신의 위치는 노이즈가 있는 ud를 통해 업데이트 된 xd입니다.
def ukf_estimation(xEst, PEst, z, u, wm, wc, gamma):
# Predict
sigma = generate_sigma_points(xEst, PEst, gamma)
sigma = predict_sigma_motion(sigma, u)
xPred = (wm @ sigma.T).T
PPred = calc_sigma_covariance(xPred, sigma, wc, Q)
# Update
zPred = observation_model(xPred)
y = z - zPred
sigma = generate_sigma_points(xPred, PPred, gamma)
zb = (wm @ sigma.T).T
z_sigma = predict_sigma_observation(sigma)
st = calc_sigma_covariance(zb, z_sigma, wc, R)
Pxz = calc_pxz(sigma, xPred, z_sigma, zb, wc)
K = Pxz @ np.linalg.inv(st)
xEst = xPred + K @ y
PEst = PPred - K @ st @ K.T
return xEst, PEstukf_estimation이 실제 UKF algorithm에 해당하는 코드입니다. UKF 역시 Prediction step과 Correction step으로 나누어져습니다. Prediction step에선 sigma point를 구하고 구한 sigma point를 이용해 ˉμ, ˉΣ를 계산합니다.
def generate_sigma_points(xEst, PEst, gamma):
sigma = xEst
Psqrt = scipy.linalg.sqrtm(PEst)
n = len(xEst[:, 0])
# Positive direction
for i in range(n):
sigma = np.hstack((sigma, xEst + gamma * Psqrt[:, i:i + 1]))
# Negative direction
for i in range(n):
sigma = np.hstack((sigma, xEst - gamma * Psqrt[:, i:i + 1]))
return sigma
sigma point를 수식에 맞게 결정하는 코드입니다. state의 차원이 4이기 때문에 sigma point는 9개가 나와야겠죠. 실제로 sigma point를 출력해보면 9개가 나오는 것을 알수 있습니다(각 column).
다시 ukf_estimation으로 돌아와 9개의 sigma point를 motion model을 통해 transform 수행, ˉμ, ˉΣ를 계산합니다. ˉμ는 weight 과 sigma point들의 곱을 통해 구해집니다.
def calc_sigma_covariance(x, sigma, wc, Pi):
nSigma = sigma.shape[1]
d = sigma - x[0:sigma.shape[0]]
P = Pi
for i in range(nSigma):
P = P + wc[0, i] * d[:, i:i + 1] @ d[:, i:i + 1].T
return P
ˉΣ는 위와 같이 계산되는데 직관적으로 covariance weight에 편차제곱을 곱하고 오리지널 covariance matrix에 더해줘 uncertainty 가 증가하는 방향으로 계산된다 라고만 이해하고 넘어가겠습니다.
Correction Step은 다른 Kalman Filter들 처럼 실제 관측값 z와 predict한 state x에서 보일거라고 생각하는 관측값 z 간의 차이를 통해 업데이트를 진행합니다. Kalman gain을 구하는 부분이 복잡하기 때문에 넘어가도록 하겠습니다.
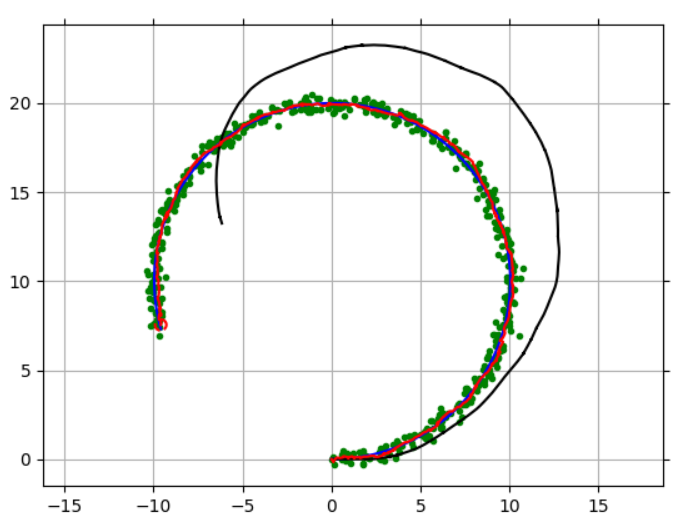
결과 plot 입니다. 검은색 실선은 Dead reckoning state, 빨간색은 ukf estimation, 파란선은 ground truth입니다. 초록색 점은 observation point라고 합니다.
'SLAM' 카테고리의 다른 글
| EKF SLAM (0) | 2021.09.21 |
|---|---|
| 여러 종류의 칼만필터(Family members of Kalman Filter)(EnKF) (0) | 2021.08.19 |
| 여러 종류의 칼만필터(Family members of Kalman Filter)(EKF) (0) | 2021.08.03 |
| 칼만필터(Kalman Filter) (0) | 2021.07.27 |
| Perspective-3-Point(P3P) Algorithm (0) | 2021.06.18 |




댓글