[SLAM] Kalman filter and EKF(Extended Kalman Filter) · Jinyong
[SLAM] Kalman filter and EKF(Extended Kalman Filter) Kalman filter와 Extended Kalman filter에 대한 설명. 본 글은 University Freiburg의 Robot Mapping 강의를 바탕으로 이해하기 쉽도록 정리하려는 목적으로 작성되었습니다.
jinyongjeong.github.io
Kalman Filter & EKF (Cyrill Stachniss)
베이즈 정리(Bayes' Theorem)
베이즈 정리(Bayes' Theorem)는 두 확률 변수의 사전확률(prior probability)와 사후확률(post probability) 사이의 관계를 나타내는, 사전확률로부터 사후확률을 구할 수 있다는 정리입니다. 이 베이즈 정리는 상태추정(State Estimation)을 하기 위해 자주 사용되고 칼만필터의 백그라운드라고 보시면 됩니다.
칼만필터(Kalman Filter)
칼만필터는 Bayes filter 중에서 자주 이용하는 필터중에 하나로 Gaussian distribution 일때, 그리고 Linear model 일 경우 효과적인 성능을 보이는 방법입니다.
Linear Model
칼만필터는 이동모델(Transition Function) 과 관측모델(Observation) 이 모두 선형이라는 것을 가정합니다.
위 Prediction 수식을 칼만필터에 맞게 표현하면 다음과 같습니다.
$$ x_t=A_{t}x_{t-1} + B_{t}u_{t} + \epsilon_{t} $$
- \( A_{t} \) : \( n \times n \) 행렬로 control 이나 노이즈 없이 시간 \( t-1 \)에서 \( t \)로의 state \( x \)의 변화를 나타내는 행렬
- \( B_{t} \) : \( n \times l \) 행렬로 control에 의한 \( t-1 \)에서 \( t \)로의 state \( x \) state \( x \)의 변화를 나타내는 행렬
가장 쉽게 생각해 볼 수 있는 것은 로봇이나 차가 정지해있을 때 control 이 없다면 시간이 지나도 state은 변하지 않을 것이고 행렬 A는 단위행렬일 것입니다. 이와 다르게 control이 없더라도 로봇이 등속도 운동을 하고있다면 컨트롤이 없더라고 state \( x \) 는 행렬 A에 의해 업데이트 됩니다.
행렬 \(B_{t}\)는 가속페달이나 브레이크를 밟아 현재 상태에 변화를 주는 것으로 생각하면 될 것 같습니다.
def motion_model(x, u):
F = np.array([[1.0, 0, 0, 0],
[0, 1.0, 0, 0],
[0, 0, 1.0, 0],
[0, 0, 0, 0]])
B = np.array([[DT * math.cos(x[2, 0]), 0],
[DT * math.sin(x[2, 0]), 0],
[0.0, DT],
[1.0, 0.0]])
x = F @ x + B @ u
return x위 코드는 pythonrobotics 에서의 motion model 함수로 인풋으로 들어오는 control \( u \)에 에러가 있다면 Prediction, 그렇지 않다면 Ground Truth state를 반환할 것입니다.
Correction
상태추정을 할 때 현재 상태를 정확히 예측하고 노이즈도 전혀 없고 control에 의해 정확히 state가 원하는 만큼 변한다면 Prediction step으로 충분하겠지만 현실은 그렇지 않습니다. 그렇기 때문에 현재 상태 \( x_{t} \)에서 주변환경을 관측하고 state를 보정하는 과정이 필요합니다.
$$ z_t=C_{t}x_{t-1} + \delta_{t} $$
- \( C_{t} \) : \( n \times k \) Matrix that describes how to mp the state \( x_{t} \) to an observation \( z_{t} \)
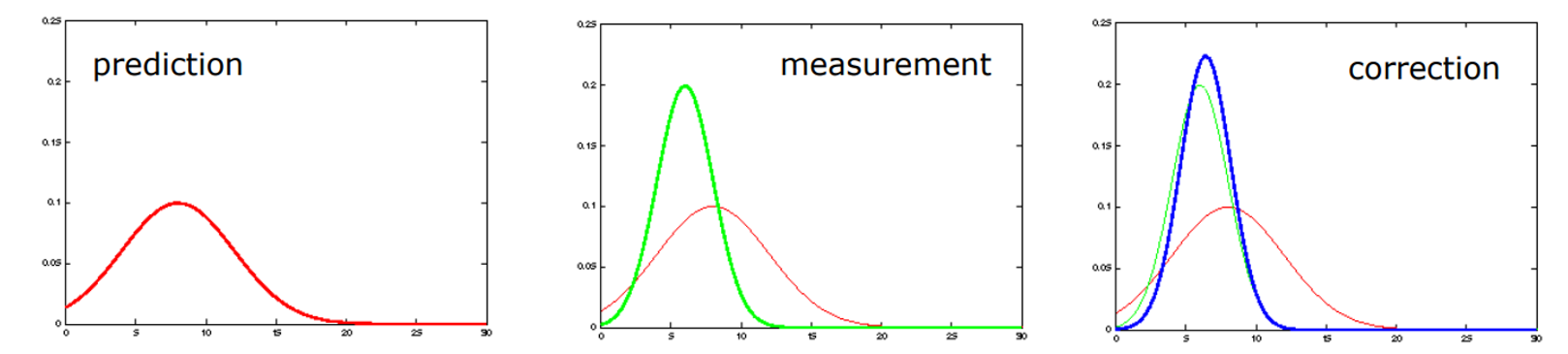
Prediction에서 구한 \( x_{t} \)은 말 그대로 예측값이기 때문에 \( x_{t} \)에서 보여질 것이라고 생각되는 관측과 실제 관측은 차이가 있습니다. Prediction은 말 그대로 예측이기 때문에 실제 측정값에 가깝게 수정된다고 합니다.
def observation_model(x):
H = np.array([
[1, 0, 0, 0],
[0, 1, 0, 0]
])
return z위 코드는 위의 Correction 식에서 error 가 없는 수식을 간단하게 코드로 옮겨본 것 입니다. 하지만 여기까지만 보면 Kalman Filter를 이용한 Localization이 어떻게 진행되는지 잘 이해가 되지 않습니다.
Kalman Filter Algorithm

실제로 추정한 현재 상태를 관측을 통해 조정하는 과정은 어떻게 이루어지는지 알아보겠습니다.
이 알고리즘의 목적은 \( t-1 \)에서 \( t \) 에서 control과 observation을 인풋으로 받아 다음 "Mean"과 "Uncertainty of Belief"를 구하는 것입니다.
Prediction Step
- Prediction Step에선 Motion model을 통해 현재 상태의 추정값 \( \bar{\mu_{t}} \) 을 구해냅니다(2). 이 과정은 직관적으로 받아들이기 쉬운것 같습니다.
- 변수가 실험 측정값인 경우 변수가 가지는 오류로 인해 함수에 오류가 전파되는 것을 error propagation이라고 합니다. 일반적으로 불확실성은 표준편차 \( \sigma \)로 정량화 된다고 합니다. Covariance Matrix \( \bar{\Sigma_{t}} \)를 (3)과 같이 구하게 됩니다.
Prediction Step을 통해 우리는 Predicted Belief 와 그에 대한 Uncertainty를 구했습니다.
Correction Step
- Prediction step 에서 계산한 \( \bar{\mu_{t}} \)을 신뢰할지, 혹은 현재 state에서의 관측을 얼만큼 신뢰할지 판단 할 수 있도록 Kalman gain \( K_{t}\)를 계산합니다(4).
- 계산한 Kalman gain을 이용해 \( \bar{\mu_{t}} \)를 조정합니다(5). \( z_{t} - C_{t}\bar{\mu_{t}}\) 는 현재 state에서의 관측에서 추정 state \(\bar{\mu_{t}} \)에서 보여질것이라고 추정된 관측의 차이입니다. 즉 실제 관측과 추정 관측의 차가 추정상태를 얼만큼 변화시킬지를 결정하는 변수가 Kalman gain\( K_{t}\) 라고 생각됩니다.
- Uncertainty를 업데이트 합니다(6).
'SLAM' 카테고리의 다른 글
| EKF SLAM (0) | 2021.09.21 |
|---|---|
| 여러 종류의 칼만필터(Family members of Kalman Filter)(EnKF) (0) | 2021.08.19 |
| 여러 종류의 칼만필터(Family members of Kalman Filter)(UKF) (0) | 2021.08.10 |
| 여러 종류의 칼만필터(Family members of Kalman Filter)(EKF) (0) | 2021.08.03 |
| Perspective-3-Point(P3P) Algorithm (0) | 2021.06.18 |




댓글