The SLAM(Simulataneous Localization and Mapping) is computational algorithm used in robotics and autonomous systems to construct a map of an unknown environment while simulateously keeping track of the robot's position within that environment. Since SLAM presupposes the movement of the robot, it is necessary to know how to represent the movement consists of rotation and translation.
Transforms Between Coordinate Systems
Considering the robot's movement in the 3d environment. Since the robot is the observer who reconizes the surrounding environment, the observed features are represented by a robot coodinate system. However, the coordinate itself is keep moving, there's a need to express it in a world coordinate system which remains unchanged.


In the above 2d example, the camera coordinate is rotated by \(\theta\) . To express the fixed point \( (x_{W}, y_{W}) \) in world coordinate as a camera coordinate system, we can easily find out:
$$ (x_{C}, y_{C}) = ((\cos{\theta} + \sin{\theta}) x, (-\sin {\theta}+ \cos{\theta})) y $$
$$ [x_{C}, y_{C}] ^{T}= R^{-1} [x_{W}, y_{W}]^T$$

Translation is much simpler than rotation.
$$ [x_{C}, y_{C}] ^{T}= [x_{W}, y_{W}]^T - t_{C}$$
If the camera coordinate is rotate and translated at the same time, then the transformation is:
$$ [x_{C}, y_{C}] ^{T}= R^{-1} ([x_{W}, y_{W}]^T - t_{C}])$$
For easy understanding, the example was given in 2d, but this applies equally to 3d. The above formula expresses the coordinate transformation of Euclidean space, but if we do some trick, the formula can be more simpler. The introduction of homogeneous coordinates and rewrite the formula, then:
$$ [x_{C}, y_{C}, z_{C}, 1]^{T} = \begin{bmatrix} R_{CW}&t_{CW} \\ 0&1 \\ \end{bmatrix} [x_{W}, y_{W}, z_{W},1]^{T} $$
Here, \(_{CW}\) means "from world to camera", \(R_{CW} = R^{-1}\) and \(t_{CW} = R^{-1}t_{C}\).
Rotation

There are several ways to express rotation including the rotation matrix. The rotation matrix requires 9 elements where there's only 3 degrees of feedom. Also the rotation matrix itself has constraints: the orthogonality. To describe rotation more compactly, we can use the rotation vector(axis-angle).
Rotation Vectors
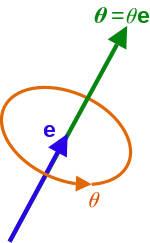
In mathematics, the axis-angle representation of a rotation parameterizes a rotation in a 3d space by 2 quantities: a unit vector \(e\) indicating the direction of an axis of rotation, and angle \(\theta\) describing the magnitude of the rotation about axis.
Then what is the relationship between the rotation matrix \(R\) and the rotation vector \(e\theta \)? The conversion from the rotation vector to the rotation matrix is given by Rodrigues' formula.
$$ R = \cos{\theta}I + (1-\cos{\theta} )ee^{T} + \sin{\theta} e^{\wedge} $$
Conversely, we can also calculate the conversion in inverse from rotation matrix to a rotation vector.
$$ \theta = \arccos{((tr(R)-1)/2)} $$
Quaternions
Quaternion can also used to represent the 3d rotation. Quaternion is widely used in the real world application because it is more compact, efficient, and numerically stable compared to rotation matrices.
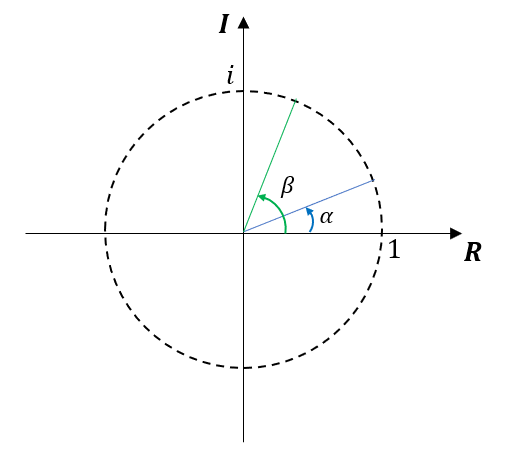
In 2d complex plane, the vector can be written in form as addition of the real and imaginary numbers. Then the multiplicating the unit vector on the 2D complex plane can represent the rotation.
$$ (\cos{\alpha}+ i \sin{\alpha})(\cos{\beta} + i \sin{\beta}) \\ = (\cos{\alpha} \cos{\beta} - \sin{\alpha} \sin{\beta}) + i(\cos{\alpha} \sin{\beta} + \sin{\alpha} \cos{\beta}) \\ = \cos{(\alpha + \beta)} + i\sin{(\alpha + \beta)} $$
Similarly, in 3d space, the rotation can be described by a unit quaternion \(\mathrm{q} = q_{0} + q_{1}i + q_{2}j + q_{3}k\) where \(i,j,k\) are three imaginay parts of the quaternion. These imaginary parts satisfy the following relationship.
$$ \left\{\begin{matrix}
i^{2} = j^{2} = k^{2} = -1 \\
ij = k, ji = -k \\
jk = i, kj = -i \\
ki = j, ik = -j
\end{matrix}\right. $$
To express the rotated point by the unit quaternion \(q\), we extend the 3d point \(\mathrm{p} = [x,y,z]^{T}\) to an imaginary qauternion \(\mathrm{p} = [0,x,y,z]^T\). Then the rotated point \(\mathrm {p}^{\prime} \) can be expressed as:
$$ \mathrm {p}^{\prime} = \mathrm{q} \mathrm{p} \mathrm{q}^{-1} $$
To convert the quaternion \(q = [s, \mathrm{v}]^{T}\) where \(s\) is the real part and vector \(\mathrm{v}\) is the imaginary part, the rotation matrix can be obtained as:
$$ \mathrm{R} = \mathrm{v}\mathrm{v}^{T} + s^{2}\mathrm{I} + 2s\mathrm{v}^{\wedge} + (\mathrm{v}^{\wedge})^{2}$$
The conversion formula from quaternion to rotation vector can be written as follows:
$$ \left\{\begin{matrix}
\theta = 2\arccos{q_{0}} \\
[e_{x}, e_{y}, e_{z}]^{T} = [q_{1}, q_{2}, q_{3}]^{T}/\sin{\frac{\theta}{2}} \\
\end{matrix}\right. $$
'SLAM' 카테고리의 다른 글
| SLAMBOOK Chapter4: Cameras and Images (0) | 2023.03.07 |
|---|---|
| SLAMBOOK Chapter3: Lie Group and Lie Algebra (0) | 2023.02.19 |
| SLAMBOOK (0) | 2023.02.13 |
| IMU Preintergration on Maniforld for Efficient Visual-Inertial Maximum-a-Posteriori Estimation(2) (0) | 2022.07.25 |
| IMU Preintergration on Maniforld for Efficient Visual-Inertial Maximum-a-Posteriori Estimation (0) | 2022.07.23 |




댓글